GEMMs (General Matrix Multiplications) are fundamental building blocks for many operations in neural networks
gemm is defined as the operation C = aAB+BC, with A and B as matrix inputs, a and b as scalar inputs, and C as a pre-existing matrix which is overwritten by the output
following convention, we will say
matrix A is an M x K matrix, meaning it has M rows and K columns
B = K x N and C = M x N
the product of A and B has M x N values, each of which is a dot-product of K element vectors. totaling at M * N * K fused multiply-adds
each FMA is 2 operations, a multiply and an add, new total is 2 * M * N * K FLOPS are required
for simplicity we are ignoring the a and b parameters for now
-------------------
to estimate if a particular matrix multiply is math or memory limited, we compare its arithmetic intensity to the ops:byte ratio of the GPU
-------------------
example: lets consider a M x N x K = 8192 x 128 x 8192 GEMM
for this specific case, the arithmetic intensity is 124.1 FLOPS/B, lower than the V100s 128.9 FLOPS:B, thus this operation is memory limited
if we increase the GEMM size to 8192 x 8192 x 8192 arithm intens increases to 2730, much higher than 138.9
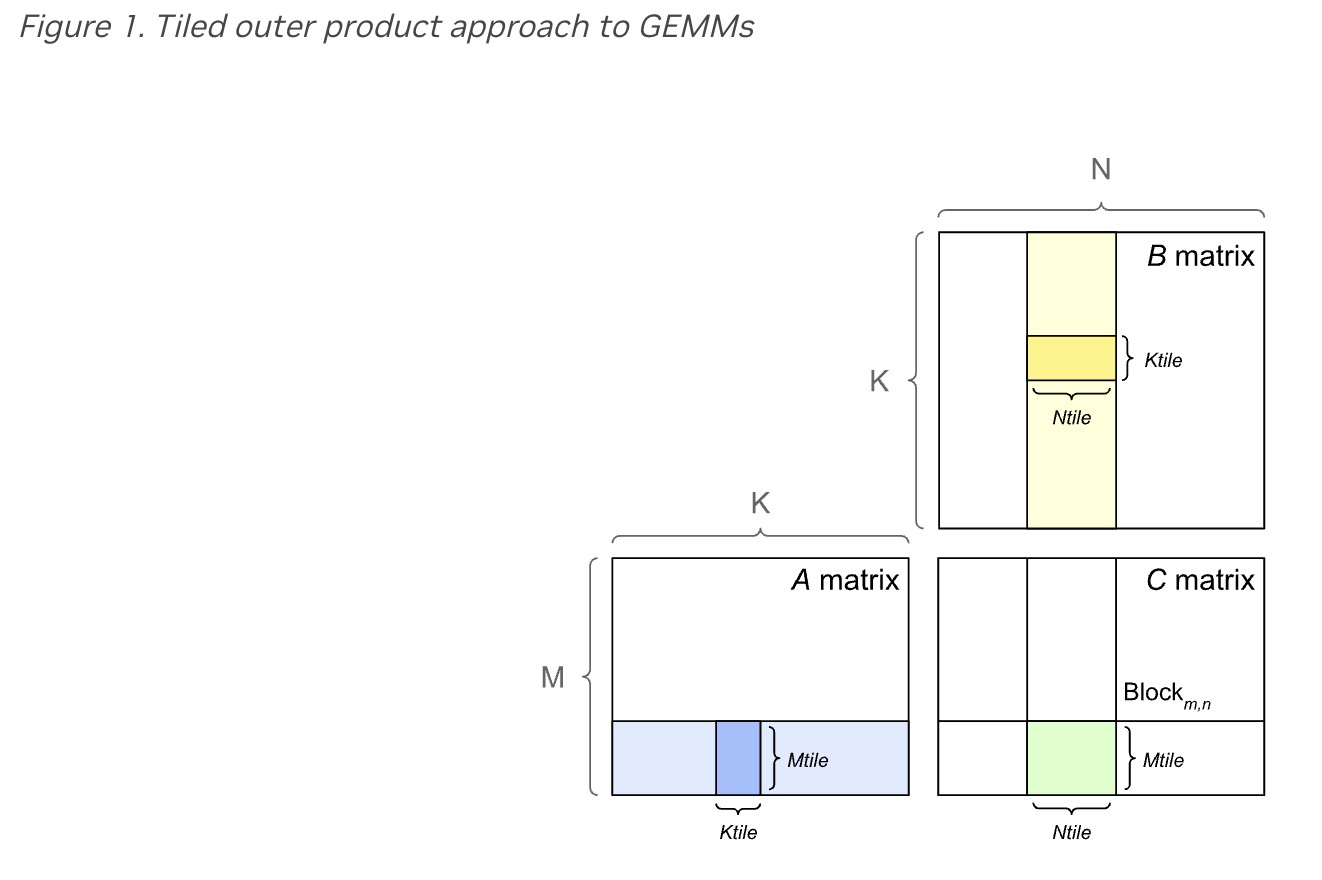
gpus implement gemm by partitioning the output matrix into tiles, which are then assigned to thread blocks
tile size in this case usually refers to the dimensions of these tiles (Mtile x Ntile)
each thread block computes its output tile by stepping through th K dimension in tiles, loading the required values from the A and B matrices, and multiplying and accumulating them into the output
----------------------------------------------------
directory